Hungarian Mathematics

The great cities are those where one can walk. I would walk all the time in London. Wherever you turn, there's history.

— General Koniev. Fail Safe (1964).

In 2003 I studied in Budapest through a program called Budapest Semesters in Mathematics. The idea was that Hungary has many great mathematicians (true) and is beautiful (true), so therefore math majors from the U.S. who want to study abroad should go there for a semester or year and learn from some great teachers. This was a good idea, and I got itchy feet near the end of my junior year of college, so in the fall of my senior year I went to Hungary. One cool thing about Hungarian mathematics is that the country's mathematicians have a long history of producing unexpected proofs using strange but entirely sound methods. Here is one such proof.

Theorem: Suppose many 1 x n tiles are put together to form a rectangle of width w and height h. This rectangle has no overlapping tiles and no gaps. Then n is a factor of either w or h.

To begin the proof, let us look at a tile. In this example, the tile is 1 x 4, but that's just to make viewing easy. It could just as well be 1 x 20. Nothing depends on this.

When I lived in Hungary, I used to walk everywhere. In Pittsburgh I had a car but only drove it when necessary, and in Tokyo I prefer foot travel for anything within several kilometers. Suppose that our tile is a special tile. To be precise, it is a garden tile, and there are two paths in the garden tile. The paths start in the corners and go along the long sides of the tile.

Suppose we put a lot of these tiles together. Then we get a big garden with many paths in it. Here is a partly complete example of one such garden. For the purposes of this proof, the garden could be this size, but it could also be smaller or larger. Regardless, this should serve to give you an idea of what we're playing with.

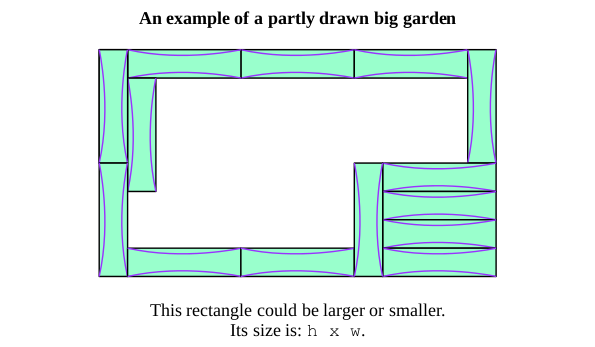
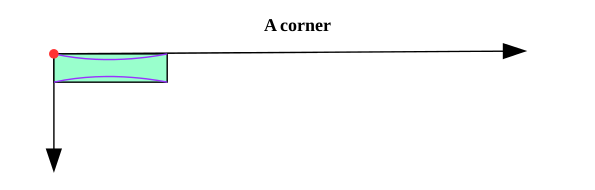
Let's look at the corner of our garden. It looks something like this, if you are happy with symmetry. That is to say, if you rotate this diagram or look at the mirror image of it, you can see all of the possible cases of a tile sitting in the corner. For simplicity, we can just focus on this one. There's a red dot marking the corner, and there is one path that connects to that corner.

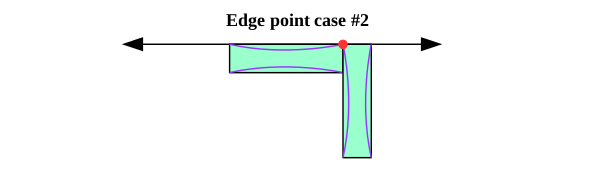
Now then, let's take a look at what happens when two tiles meet along an edge of our large garden. The two tiles could be parallel (Edge point case #1) or perpendicular (Edge point case #2) to each other. Note the red dot. There are two paths that meet at it.

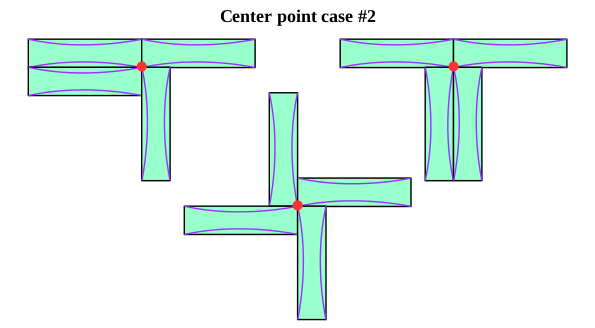
Next let's consider the points in the center of the garden somewhere. Sometimes four corners come together to form a point (Center point case #1 and Center point case #2). In these examples, there are four paths at the red dot.

In the remaining cases (Center point case #3), two corners of two tiles make a point, and they meet somewhere in the middle of a third tile. In these cases, there are two paths at the red dot. And now that we've looked at all the examples we need.

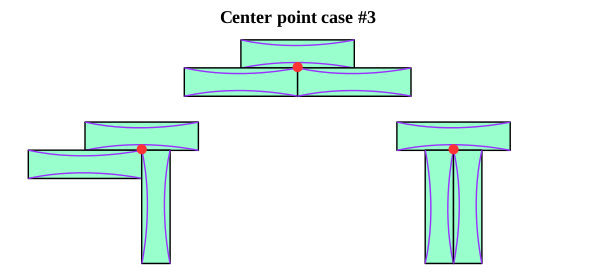
Observation: There are no other examples. We described all possible corner points, edge points, and center points using the above examples. This is of course subject to rotation and reflection of the sample cases, but nothing we do is dependent on how you view the garden, so rotating and reflecting doesn't break anything.

Now let's take a walk in our garden, starting in one of the corners and ending ... sometime. We'll take a walk, but with only one stipulation. We won't ever go down the same path twice. That would be boring. I don't know how long the walk is, but we have a lot of time, so off we go.

Claim: We can't get stuck along the edges or in the middle of the garden. All the points on the edges have two paths, which means if we take one in, we take the other out, and we never return there. The points in the middle have either two or four paths. If they have two, we can go there at most once (in and out), and if they have four, we can go there at most twice (in and out, and later in and out), but just as with the edge cases, we can't get stuck.

Claim: We have to end up at a corner. We started walking from a corner, we can't get stuck in the middle or along an edge, and we keep going until something happens. We never take a path twice, so eventually we run out of places to go. The only possible place we can stop, then, is a corner.

But this is about all we need. Suppose I start in the upper left corner and end in the upper right corner. While walking through my garden, I went left and right many times, perhaps, but each time was an increment of n. Suppose I went left l times and right r times. Then w = n * (r - l), so n is a factor of w. Similarly, suppose I end up in the lower left corner, going down d times and up u times. Then h = n * (d - u), so n is a factor of w. If I were to end up in the lower right corner, by the same argument, n is a factor of both h and w.

Q.E.D.

Bethlen Gábor ter. My old apartment building. Picture by Attila Terbócs.

Cellular Automata

Suppose you have a board, like an Othello board, for example, where each square can be one of two colors. Along with that board there are some basic rules. Each turn, you apply the basic rules, and a new board is produced. Maybe some of the squares change color once or many times. Maybe they all do. That depends on the board and the rules. This type of setup describes a cellular automaton. The most famous example, though probably not the most commonly studied, is Conway's Game of Life. Here, we'll look at a simpler example.

Suppose I have a board with red and gray squares. Here I'll look at some 3 x 3 examples, though the board could be of any size. For this board, there is one rule.

Rule: If there is a gray square with two or more red squares directly adjacent to it, it turns red. By "adjacent" I mean only above, below, to the left, or to the right.

The above is an example board with three red squares, and by the third round it's entirely red. The next one also starts with three red squares, but it takes five rounds to turn entirely red.

The third one starts with three red squares and ends with six red squares. Even if we waited for the fourth or fifth round, or longer, nothing would change. It doesn't become entirely red.

These three examples don't change at all. They have only two or three red squares, and they stay like that.

Rules: Here is a graphical representation of the rules. In this picture, there is a gray square with red squares on the left and right. In one round, that gray square changes to red. Note that this could also happen vertically. There's no need to draw that — just imagine the same picture rotated ninety degrees.

Here are two examples that are essentially the same. In the first, the gray square is bordered by red squares on the left and bottom. In one round, it turns red. In the second picture, both gray squares are bordered by red squares on two sides, so they both turn red.

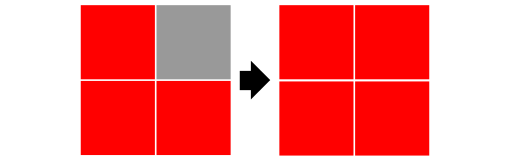
Theorem: For an n x n board, if there are fewer than n red squares at the start, it will not turn entirely red.

Proof: Let us consider the red perimeter of a board. We define the red perimeter as the number exposed red edges in that board. For example, a 3 x 3 board with eight gray squares and one red square has a perimeter of 4, because the red square has four sides. A 3 x 3 board of all red squares has a red perimeter of 12, because the exposed red edges are the four sides of the large square. Now we look at what effect applying the rule has on the red perimeter.

In the above case, the initial state has a red perimeter of 8, as does the new state. This is also true for the following two cases.

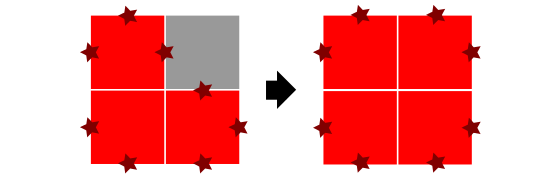
As we can see, these are the only possible cases, up to rotation and reflection, and the perimeter stays the same in all of them. Actually, we don't know if there are red squares on the other side of these gray squares, so it's possible the red perimeter could decrease — just imagine a board with a gray square in the middle surrounded by eight red squares. But in no case can the red perimeter increase, as these illustrations show us.

An all red n x n board has a red perimeter of 4n. Since each round the red perimeter stays the same or decreases, to obtain an all red board, the starting board has to have at least a 4n red perimeter, too. Arranged optimally, this requires n tiles, provided they don't border each other, or more if they do. If there are any fewer, the board cannot become all red.

Q.E.D.

Travel

In my study abroad program there were about fifty students. Most of us were from the U.S., and maybe all of us were from U.S. universities. On weekends, seeing as how the trains were so cheap, we frequently traveled to neighboring cities and countries. That fall I visited Slovenia, Slovakia, Czech, Austria, Croatia, and Poland. It has been a decade, and my memories have no doubt blurred, but here are some things I remember...

Vienna

The cleanest city was Vienna. Hungary hadn't been properly cleaned in a long time, and in the summer the street smell in Hungary was unbecoming. At night, people used dark corners as urinals. It took me about a week to stop using my nose to breathe. And later, once the fall came and the temperature dropped, there was no issue. But Vienna was clean, and very nice for walking. We know that of course English was partly derived from German, and though I can only speak a few sentences of guidebook German, from time to time there there were signs that I read and understood quite clearly.

Prague

In Czech we visited Prague, which is a very picturesque city. It feels small and majestic, somehow, though I think the size is not so small. We traveled on Saturdays and Sundays because there was no class on the weekends, you know. On Saturday, and I suppose this was late September sometime, we went to some museums and listened to a classical music concert. On Sunday, we took a random bus a random number of stops and walked back to the city center. Probably Prague and Budapest are the two most remarkable cities in eastern Europe, for your average American sightseer.

Slovenia

Three of us went to Slovenia for three days. As I recall, we spent a day in the mountains, a day at a cave, and a day in the capital. The capital, Ljubljana, is nice enough but not particularly noteworthy. There is a castle on a hill, like there is in every European city of note. The Skocjam Caves, though, were quite nice, and the mountains were beautiful. We were there in the fall sometime, and snow had begun to fall, but it hadn't yet stuck. One of my friends took some pictures of Lake Bohinj in the Julian Alps.

Slovakia

The other week I emailed Ján Máté with a technical question about some software he writes (CalDavZAP). I mentioned that I'd been to Bratislava, where he lives, for one day ten years ago. He said Budapest and Prague were better cities. I suppose that's true, for sightseeing in general. On the other hand, the day I spent in Bratislava was enjoyable. It was sunny, as I recall, and we started off with coffee at a street-side cafe. We had no guidebook, which was a clear case of poor trip planning, so we walked around until the late afternoon. For lunch we went to a German restaurant, or so it turned out, but we had no idea because we couldn't read the menu and ordered food by pointing at random items on the list. I ordered a sausage and potato dish that was as tasty as it was greasy, and it was greasy as hell.

Croatia

My brother George once said that if it takes longer to get to a place than the time you spend at the place, maybe you're doing something wrong. In certain cases, I disagree. Hiking and motorcycle trips, for example, are activities where the journey is the goal, and the destination is just icing on the cake. But by and large, George was right. Back then, though, I didn't realize this, and our trip to Croatia was largely a time sink. We decided to go fairly far south along the Adriatic Sea, which was a good choice, because the Adriatic Sea has beautiful, clear, light blue water. But it was a bad choice, because the trip there took sixteen hours. My roommate Alex once accidentally dropped his cell phone over the edge of a ferry in the Adriatic, and he said he could see it perfectly as it sank down into the waters. He said it was beautiful. He also said he could find better ways to throw away two hundred dollars. To get to Split, a nice town on the Adriatic that a friend recommended, we took a night train. But there was a problem with the tracks ... maybe a rock slide? ... so we switched to a bus halfway down. This added several hours to our already lengthy journey. In fact there are other nice towns along the sea in northern Croatia that would have been much more reasonable destinations. The next morning it started raining, and the rain continued all weekend. As I recall, we looked at the beach and some Roman ruins. Perhaps we had pizza for lunch or dinner. We took the train home Sunday afternoon.

Krakau

One day I went to Poland. On the way, a young woman from Mexico came into my car on the train. I think she was worried about traveling alone, which was apparently justified, because that night when we were both asleep on the train someone came in and stole her camera, video camera, and passport. I used my bag as a pillow, and my passport was in my pocket, but her stuff was on the overhead rack, and apparently it made a nice haul for the thieves in southern Poland. Roosevelt said every cloud has a silver lining, and I don't know if that's true, but on the positive side, her passport was stolen in Poland, and she was meeting Mexican friends in Poland. At least she had someone to join her on a journey halfway across the country to the nearest Mexican consulate. Her friends insisted on searching my bag just to make sure that I wasn't the thief. I never saw her again. From Krakow, it's a thirty minute trip to Auschwitz and Birkenau. Auschwitz was a concentration camp area during World War II, as you may know. The largest death camp in the Nazi empire was Birkenau, and when the Nazis were withdrawing, they tried to cover up their tracks by knocking down the brick ovens and burning down the wood buildings. Rather than build a museum, the Polish government chose to leave the area largely as it was in 1945 at the end of the war. When you go there, you see a large, large field. There used to be hundreds of wood huts, but those all burned down. There's a pile of bricks in the far corner, a kilometer's walk from the entrance. Concrete fence posts and barbed wire fence are largely still standing. As you walk around the vast quietness, you can try to imagine, if you like, what kind of horrible place it must have been. In the afternoon, I returned to Krakow and after dinner took the overnight train home. One day in that city was enough for me.

Budapest

Budapest has a ballet and an opera. Both perform several days a week for most of the year. The cheap seats are quite cheap but entirely worth the money. I couldn't afford the good seats. Seats sell out a week or month in advance, depending on the show and date, so reservations are essential. My friends and I dressed up and went to the ballet and opera perhaps half a dozen times over the semester.