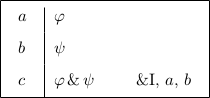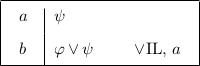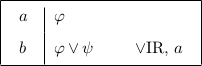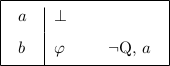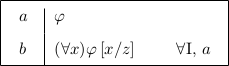Strategic Proof Tutoring in Logic

Abstract

In the mostly online course Logic and Proofs, students learn to construct natural deduction proofs in the Carnegie Proof Lab, a computer-based proof construction environment. When given challenging problems, students have difficulty figuring out how the premises connect with the conclusion. Through use of a modification of the intercalation calculus, a strategy is provided to students on choosing which inference rules to apply in various circumstances. The strategy is also implemented in AProS, an automated theorem prover. In this thesis I describe how the Carnegie Proof Lab has been extended to provide three different modes of dynamic strategic proof tutoring, using AProS to help generate hints. The Explanation Tutor explains how tactics apply to partial proofs, the Walkthrough Tutor guides students through strategically constructed proofs, and the Completion Tutor provides on-demand strategic hints. When properly used, they should provide students with support in learning how to construct proofs in a strategic fashion.

Chapter 1 Background

For our project it was crucial to have a “theorem proving system” that can provide advice to a student user; indeed, pertinent advice at any point in an attempt to solve a proof construction problem. To be adequate for this task a system must be able to find proofs, if they exist, and follow a strategy that in its broad direction is logically motivated, humanly understandable, and memorable. [Sieg and Scheines, 1992]

Logic and Proofs is an introduction to formal logic. This online course provides a proof construction environment. AProS, an automated theorem prover, provides the basis for automated dynamic hint generation as part of the proof construction process. The core of my work, then, is putting these two components together in a sensible and effective fashion, providing a demonstration of how one can harness an expert system in order to provide automated tutoring as well as a useful addition to education software that is and will continue to be used by students every semester.

1.0.1 Acknowledgments

Some of the ideas here go back a long time; the first papers on the topic were written by Sieg and Scheines; e.g., Sieg and Scheines [1992, pp. 154]. I make extensive use of AProS, written in large part by Joe Ramsey, and later rewritten by Tyler Gibson. When I needed new features or changes to AProS and the Carnegie Proof Lab, Tyler Gibson and Davin Lafon provided a great deal of assistance. The technical groundwork for implementation of the tutor was laid by Jesse Berkelhammer and Davin Lafon. Producing a good tutor involved discussions with many of the aforementioned individuals, as well as Marjorie Carlson, Iliano Cervesato, Akiva Leffert, Jason C. Reed, and Paul Zagieboylo. Finally, the entire project exists because of Sieg, who has kept me moving in the right direction.

1.1 An overview of the Logic and Proofs course

Logic and Proofs [Open Learning Initiative website, AProS website] is an online logic course, developed at Carnegie Mellon University (CMU) since 2003. The course covers propositional and first-order logic, motivating each of these with natural language examples of arguments captured in said logics. The online text is composed of HTML with graphics, Flash videos [Flash website] and exercises. Each Flash exercise is designed either to elucidate a restatement¹ — or make use² — of a recently presented concept. It also makes use of the Carnegie Proof Lab (CPL), a natural deduction problem solving environment.

1.1.1 History of the Logic and Proofs course

In the early nineties, the Carnegie Proof Tutor project [Sieg and Scheines, 1992, pp. 154] explored the effects of different computer-based proof construction environments. At that time, Sieg was also developing the intercalation calculus, a formalization similar in character to the sequent calculus, to enable automated proof search in natural deduction. In the latter half of the decade, the intercalation calculus was extended from propositional to first-order logic [Sieg and Byrnes, 1998]. AProS, short for “automated proof search”, is an automated theorem prover that makes use of the intercalation calculus in proof search. The Logic and Proofs project began in 2003. On one side it involved developing an online logic course, complete with the Carnegie Proof Lab, a natural deduction proof construction environment. On the other side, it involved implementing AProS in Java. In 2003 and until recently, some of the libraries in AProS were shared with the Carnegie Proof Lab, but this was the extent of the overlap. While the Carnegie Proof Tutor does contain “tutor” in the title, it is only recently that we have implemented tutoring in the Carnegie Proof Lab, and in this way AProS and the Carnegie Proof Lab have been brought closer together [Sieg, 2007].

1.1.2 Course structure

The online Logic and Proofs material can be used in various ways: as a completely online course that meets only for exams, as a course that meets once a week (as done at CMU), as a course meeting two or three times a week with the online text used instead of a paper textbook, or some variation on the above. The online material is organized and presented in a fashion designed to lessen the need for lectures, so instructors can use class time for review, group work, student presentations, or other non-lecture activities. As offered at CMU, Logic and Proofs is a general elective with no prerequisites. The class has thirteen chapters — an introductory chapter on statements and arguments is followed by six chapters for propositional logic and six more for first-order logic. Chapters are typically completed weekly. In each section, there are chapters devoted to motivation and syntax of the language, chapters devoted to semantics and finding counterexamples with truth trees, and four chapters involving proofs. By the end of five chapters (five weeks, then), students are expected to be able to produce reasonably complex and long proofs³ in propositional logic. The basic rules of propositional and first-order logic have their respective chapters, as do derived rules and strategies. Other major topics include metamathematics and Aristotelian logic. There are homework assignments at the end of each chapter as well as Learn by Doing exercises, either in Flash or using the Carnegie Proof Lab.

1.2 Formal Logic

Logic and Proofs covers natural deduction proofs in classical sentential and first-order logic. I use fairly standard formal logic notation, but because notation often varies in subtle and important ways, it is worth reviewing.

Propositional formulas: Atomic formulas are upper-case letters A, B, . . . , Z. Compound formulas are produced recursively. Given any two formulas ϕ and ψ, there are compound formulas ¬ϕ, (ϕ & ψ), (ϕ ∨ ψ), (ϕ → ψ), and (ϕ ↔ ψ). A contradiction is represented by the falsum, ⊥. Logic and Proofs diverges from the presentation in Sieg and Byrnes [1998] in that ⊥ is used to represent a contradiction and is often used in place of the contradiction itself. However, ⊥ is a special formula in the language⁴, and can only be used as noted.
Variables for propositional formulas: Variables that range over formulas are lower-case Greek letters — typically, ϕ, ψ, and ρ. Unless explicitly stated, variables do not represent ⊥; one should use ⊥ itself as needed.
Quantifiers: Lower-case letters a, b, . . . , z are terms. There are two types of terms: constants, a, b, . . . , s, and variables, u, v, . . . , z. For convenience, we reserve t for terms that could be constants or variables. Given any formula ϕ and any variable x, one can form the first-order compound formulas (∀x)ϕ and (∃x)ϕ. If an instance variable is not quantified in a formula ϕ, it is free in ϕ; otherwise, it is bound. The rules for producing compound formulas in propositional logic also apply in first-order logic.
Predicates: Upper-case letters A, B, . . . , Z followed by parentheses containing zero or more terms are predicates. Zero-place predicates behave just like propositional atomic formulas, and I often drop the parentheses after such predicates.
Subformulas: For any formula ϕ, ϕ is a subformula of ϕ. For any formula ρ of form (ϕ & ψ), (ϕ ∨ ψ), (ϕ → ψ), or (ϕ ↔ ψ), ϕ and ψ are subformulas of ρ. ϕ is a subformula of ¬ϕ. As for first-order logic, ϕ with all free instances of x replaced by any term t is a subformula of (∀x)ϕ and (∃x)ϕ for any variable x. As well as being reflexive, the subformula property is transitive; that is, if ϕ is a subformula of ψ and ψ is a subformula of ρ, then ϕ is a subformula of ρ. Another useful notion is that of a strictly positively embedded subformula. Strictly positively embedded subformulas are defined just like subformulas with the following exceptions: for any formulas ϕ and ψ, ϕ is not a positively embedded subformula of ¬ϕ or (ϕ → ψ). If ϕ is a positively embedded subformula of ψ, we say ϕ is positively embedded in ψ. A positively embedded subformula that is a negation is called a positively embedded negation. Let ϕ ◁ ψ mean that ϕ is a positively embedded subformula of ψ.
Variables for first-order formulas: Variables for first-order logic are similar to those for propositional logic. Lower-case Greek letters are used, and the interior of a predicate is expounded as necessary. For example, ϕ (a, b, c) can represent A (a, b, c) or E (a, b, c) but not A (b, c). If the interior of the predicate is irrelevant, the formula may be represented as just ϕ.

For the above syntactic objects, if one is running low on them, one can subscript them with natural numbers — that is, x₀, ϕ₁₀₀, and similar syntactic objects are permissible. In Logic and Proofs, the material is divided strictly into propositional and first-order sections, so terms, predicates, and quantifiers are all introduced at roughly the same time.

1.2.1 Natural deduction proofs

A proof is a finite sequence of formulas with several constraints. The first zero or more formulas are the premises, and the last formula is the goal. Each formula has a corresponding justification, where a justification could be that the formula is a premise, assumption, or the result of an inference rule; these are described in the next section. Additionally, every formula is in a subproof, which is determined by the set of premises and assumptions upon which the formula relies. For a proof or partial proof, let us define the assertion as the original premises and conclusion of it. Logic and Proofs uses Fitch diagrams⁵ to present proofs. When constructing proofs, Fitch diagrams have some advantages over Gentzen’s tree notation, but because the recursive construction of a tree is easier to describe than that of a Fitch diagram and many properties of proofs are described recursively, tree proofs are often easier to use and understand when describing properties of proofs. Converting to and from a Fitch diagram to a tree proof is conceptually easy, so I switch notation as clarity dictates.

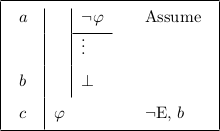
In Logic and Proofs, students bridge the gap from the premises of an argument to its conclusion using inference rules⁶. The two big questions, closely connected, are “what inference rules can be applied right now?” and, given that list, “how shall I decide the order in which to try them?”. The latter question is addressed in Section 1.2.3; as for the former — close in keeping with the presentations in Gentzen [1969] and Prawitz [1965], Logic and Proofs has the following basic rules: Conjunction Elimination Left (&EL), Conjunction Elimination Right (&ER), Conjunction Introduction (&I), Disjunction Elimination (∨E), Disjunction Introduction Left (∨IL), Disjunction Introduction Right (∨IR), Implication Elimination (→E), Implication Introduction (→I), Negation Introduction (¬I), Negation Elimination (¬E), and Falsum Introduction (⊥I)⁷. By replacing Negation Elimination with ex falso quodlibet, intuitionistic logic is obtained⁸. By adding Universal Elimination (∀E), Universal Introduction (∀I), Existential Elimination (∃E), and Existential Introduction (∃I), first-order logic is obtained. See Appendix A for precise formulations of the inference rules. Each of the above rules is classified either as an elimination rule or an introduction rule by its name, except that Negation Elimination is an introduction rule and Falsum Introduction is an elimination rule. Also, the above rules can be used from the premises working towards the goal (forwards), from the goal working towards the premises (backwards), and working directly from both the premises and the goal (forwards-backwards). An example of a forwards move is found in Table 1.1.

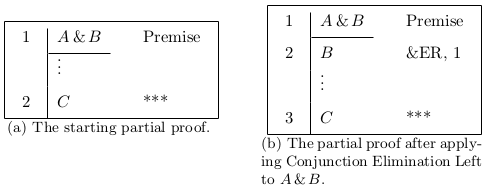
Figure 1.1: An example of a forwards move.

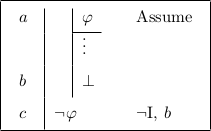
Because forwards moves are dependent only upon the premises or assumptions used in the rule, it is easy to use forwards rules that produce unwanted or unneeded lines in a partial proof. One can work backwards from a goal, so we mark open questions — that is, goals not yet proven — with *** to the right. A completed proof is one with no open questions; a partial proof, by contrast, is one with at least one open question. An example of a backwards move is found in Figure 1.2.

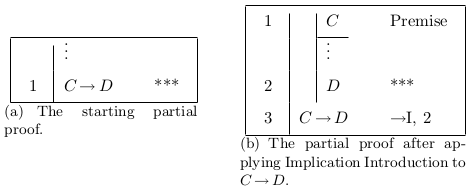
Figure 1.2: An example of a backwards move.

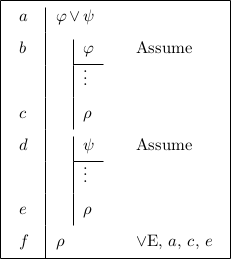
Because backwards moves are fairly well determined, except for Disjunction Introduction Left and Disjunction Introduction Right, there is little ambiguity in determining which rule to use. Forwards-backwards moves involve selecting a premise and a goal. Application of the rule produces one or two subproofs with an assumption and goal in each. These rules are sometimes called closed scope elimination rules or simply closed scope eliminations, and the conclusion of such a rule may have no syntactic connection with the premise. An example of a forwards-backwards move is found in Figure 1.3.

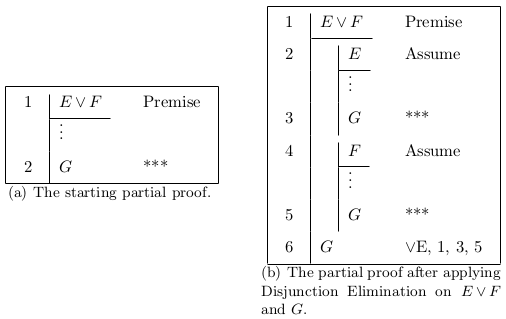
Figure 1.3: An example of a forwards-backwards move.

A proof or partial proof is p-normal if no formula occurrence in it is the major premise of an elimination rule as well as the conclusion of either an introduction rule or Negation Elimination [Sieg and Byrnes, 1998, pp. 68]. In a small shift⁹ from Sieg and Byrnes, I define the adjacency condition as follows. The adjacency condition is satisfied so long as there there is no rule application of Falsum Introduction such that either the major premise of that application is the conclusion of Negation Introduction or Negation Elimination¹⁰. See Figure 1.4 for examples of non-normal proofs.

Figure 1.4: Non-normal proofs.

If a proof or partial proof is p-normal and satisfies the adjacency condition, it is by definition normal; this is equivalent to Prawitz’s definition [Sieg and Byrnes, 1998, pp. 68]. As discussed later, non-normal proofs and partial proofs can be undesirable in proof construction; see also Prawitz [1965] and Sieg and Byrnes [1998].

1.2.2 The intercalation calculus

. . . there was one question that disturbed [the student] again and again: “Yes, the solution seems to work, it appears to be correct; but how is it possible to invent such a solution? . . . and how could I invent or discover such things by myself?” [Polya, 1945].

In order to shrink the search space and avoid detours in natural deduction proof construction, rule use can be restricted, either formally, by not allowing undesirable moves, or informally, by recommending only desirable moves. To this end, we reexamine the intercalation calculus, a modification of the sequent calculus that more cleanly captures proof search in natural deduction. This presentation is similar to Sieg [2005], Sieg and Byrnes [1998], Sieg [1992], and Sieg and Scheines [1992], except that it is more restrictive. Here we want to use the intercalation calculus in a limited way — to capture a particular strategic approach to proof search and construction which will be discussed in Section 1.2.3. Consequently, we formulate the inference rules to directly mirror this approach.

The intercalation calculus¹¹ can be formulated in production rules that operate over triples of the form Γ ; n ◀ ϕ ? G or Γ ; · ? G, shown below. Γ is the set of premise and assumption formulas, G is the goal formula, and n ◀ ϕ is an extraction — an occurrence of the goal, n, strictly positively embedded in ϕ. Let · denote the empty extraction. We call the triple on the right of the ⟼ the premise of the rule and the triple on the left the result of the rule. The intercalation calculus rules are expressed as rewrite rules; we start with the ↑ and ¬ rules.

&↑	Γ ; · ? (ϕ & ψ)	⟼	Γ ; · ? ϕ and Γ ; · ? ψ.
∨_i↑	Γ ; · ? (ϕ₁ ∨ ϕ₂)	⟼	Γ ; · ? ϕ_i for i = 1 or i = 2.
→↑	Γ ; · ? (ϕ → ψ)	⟼	Γ ∪ {ϕ} ; · ? ψ.
¬↑	Γ ; · ? ¬G	⟼	Γ ∪ {G} ; · ? ⊥
¬_C	Γ ; · ? G	⟼	Γ ∪ {¬G} ; · ? ⊥.
⊥(𝓕)	Γ ; · ? ⊥, ϕ ∈ 𝓕(Γ)	⟼	Γ ; · ? ϕ and Γ ; · ? ¬ϕ
∨⇂^∗	Γ ; · ? G and (ϕ ∨ ψ) ∈ Γ	⟼	Γ ∪ {ϕ} ; · ? G and Γ ∪ {ψ} ; · ? G.

For ⊥(𝓕), let 𝓕(Γ) denote the set of unnegated formulas whose negations are positively embedded subformulas in Γ. ¬_C may not be used when the goal is ⊥. To start using ↓ rules, the goal must be positively embedded in a premise or assumption — this is specified by n in n ◀ ϕ. While ◁ is used for strictly positive subformulas, ◀ is used for strictly positive subformula occurrences, so n ◀ ϕ is more restrictive than n ◁ ϕ. Only the ↓ rules can be used on triples with non-empty extractions. To stop using the ↓ rules, n must be obtained. Because n is a particular instance of G, the exact sequence of ↓ rules is determined when the first one is applied. This corresponds to a partial natural deduction proof where one notes that the goal is positively embedded in a premise or assumption and uses elimination rules to get to the goal.

E↓	Γ ; · ? G and ϕ ∈ Γ and n is an instance of G and n ◀ ϕ	⟼	Γ ; n ◀ ϕ ? G.
&_i↓	Γ ; n ◀ (ϕ₁ & ϕ₂) ? G	⟼	Γ ; n ◀ ϕ_i ? G for i = 1 or i = 2.
→↓	Γ ; n ◀ (ϕ → ψ) ? G	⟼	Γ ; · ? ϕ and Γ ; n ◀ ψ ? G.
∨_i↓	Γ ; n ◀ (ϕ₁ ∨ ϕ₂) ? G	⟼	Γ ∪ {ϕ_i} ; · ? G and Γ ∪ {ϕ_j} ; n ◀ ϕ_j ? G for i ≠ j.

For completeness, though, we cannot only consider eliminating disjunctions in Γ — we must also consider disjunctions that are strictly positively embedded in formulas in Γ. The following inference rule, ∨⇂, is a generalized version of disjunction elimination — ∨⇂^∗ is a special case of ∨ when the disjunction is in Γ, so ∨⇂^∗ can be removed from any further considerations.

∨⇂	Γ ; · ? G and ρ ∈ Γ and n is an instance of (ϕ ∨ ψ) and n ◀ ρ	⟼	Γ ; n ◀ ρ ? (ϕ ∨ ψ) and Γ ∪ {ϕ} ; · ? G and Γ ∪ {ψ} ; · ? G.

Given a goal G and a set of premises, Γ, we can produce the search space for an intercalation calculus proof of the possibly-true assertion Γ ⊢ G. Start with Γ ; · ? G and do the following recursively. For each rule that could be applied to the current node Γ_c ; n_c ◀ ϕ_c ? G_c, so long as it would not violate the adjacency condition and would not be a repeated question¹², make a branch above it to each premise, Γ_n ; n_n ◀ ϕ_n ? G_n, and then visit that premise. For an example of an intercalation calculus tree, consider tertium non datur.

The root is fully expanded, with branches for ∨1↑, ∨2↑, and ¬C. Each of these nodes, however, has not yet been expanded — ¬C could be used on all three¹³, ¬↑ could be used on the middle, and ⊥(F ) could be used on the right. Once such a tree has been fully expanded, it can easily be evaluated. For any leaf Γ ; n ◀ ϕ ? G, the leaf is marked Y if G ∈ Γ or G equals ϕ, and it is marked N otherwise. Starting from the leaves, the tree is evaluated¹⁴ recursively down to the root, where each node is marked Y if the dependency or dependencies of at least one of the rules producing a node above it is satisfied, and N otherwise¹⁵. If the root is marked Y, the argument is provable, otherwise it is not. When used in this fashion in proof search, the intercalation calculus with the above algorithm provides a complete search procedure, and it will provide only normal proofs. In practice, it may not be necessary to produce the entire search space tree if the root can be marked Y without doing so. Because of the correspondence between intercalation calculus rules and natural deduction inference rules, a search space tree with the root marked Y — a tree for a theorem — readily provides a natural deduction proof. To obtain one of these proofs — there may be several — work from the root upwards. From the current node, select one rule application that is marked Y. Retain it and then traverse its children, repeating as necessary. This produces a smaller tree from which, by retaining just the goal and mapping the rules in the obvious fashion, a natural deduction proof is obtained.

1.2.3 Strategic proof search in natural deduction

We define the four following tactics for proof search in natural deduction.

Extraction: Use one or more forwards elimination rules from a premise or assumption towards a goal. This corresponds to using the ↓ intercalation calculus rules.
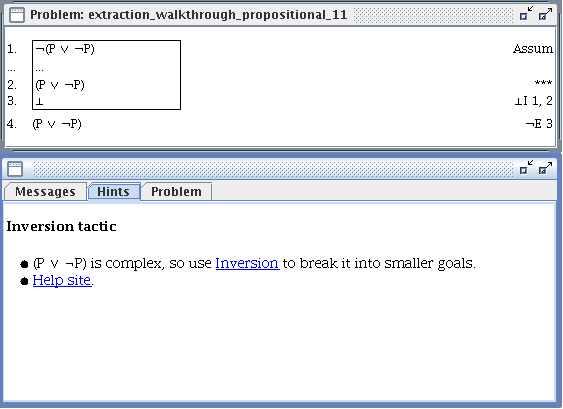
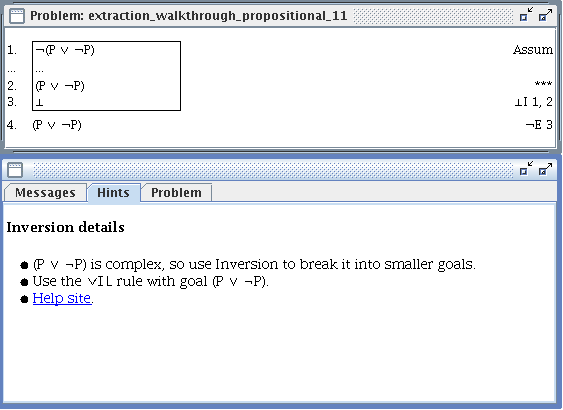
Inversion: Use a backwards introduction rule on a complex goal. This corresponds to using the ↑ intercalation calculus rules.
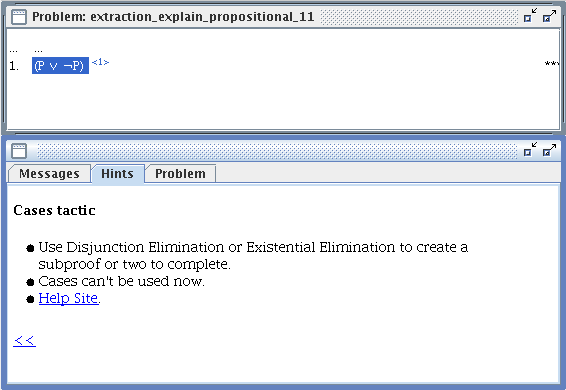
Cases: Use Disjunction Elimination from a premise, assumption, or a disjunction strictly positively embedded in a premise or assumption¹⁶ to a goal. This corresponds to using the ∨ intercalation calculus rule.
Refutation: Use Negation Elimination on a goal. This corresponds to using the ¬C intercalation calculus rule.

Strategic proof search says to try the above tactics generally in the listed order, skipping tactics that would lead to partial proofs that violate the adjacency condition or repeated questions. This, then, is a heuristic or rule for deciding what branch of the intercalation calculus search space to pursue first. If the entire search space has been traversed and no proof is found, the argument is invalid. For some invalid arguments in first-order logic, this may not happen in finite time. In automated proof search, the strategic approach has various strengths. First, the proofs for which it searches have the subformula property, which places bounds on the search space. Second, extraction rules are restricted and only used when the goal is obtainable from the premise [Sieg and Scheines, 1992]. In some circumstances, this can noticeably speed up the search process [Sieg and Field, 2005]. Strategic proof search is useful for both humans and computers engaged in proof search. For computers, applying the tactics in order provides a search algorithm for traversing the search space, expressed by the AProS proof generator [AProS website]. For humans engaged in proof search, the strategic approach can also be used as an algorithmic proof construction procedure. Students first learning how to construct natural deduction proofs can have difficulty determining how to proceed, so having a procedure for completing a proof can be useful — classroom observation suggests that even students with some experience can have difficulty proving tertium non datur, ⊢ ϕ ∨ ¬ϕ, DeMorgan’s Law, ¬(ϕ & ψ) ⊢ ¬ϕ ∨ ¬ψ, and Peirce’s Law, ⊢ ((ϕ → ψ) → ϕ) → ϕ. The strategy may also be used as a valuable heuristic, in the Polyaic sense of the term [Polya, 1945]. Much of the time, students look at the section of a partial proof and see immediately how to finish it. In that case, there is no need to explicitly follow the algorithm. On the other hand, students often do not know what to try next or are in a state where they need to backtrack. Thinking strategically can help them properly determine what actions they might want to take or how much they need to backtrack.

1.2.4 The extraction rule

Inversion, cases, and refutation all require exactly one rule application to use, but extraction requires one or more rule applications, making the tactic harder to learn and use. To make the extraction tactic easier to use in the Carnegie Proof Lab, I introduce the extraction inference rule. To use an extraction, select a premise and a goal that is positively embedded in the premise. Applying the rule will use all of the elimination rules necessary to get to the goal. For each rule application that has a minor premise ϕ, ϕ is added to the partial proof as an open question. See Figure 1.5 and 1.6 for examples of extraction.

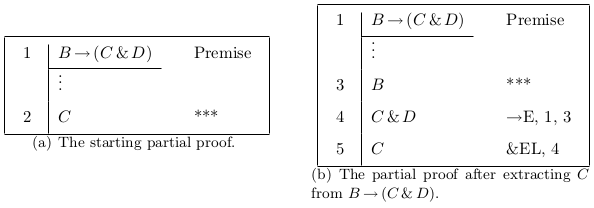
Figure 1.5: Using the extraction rule.

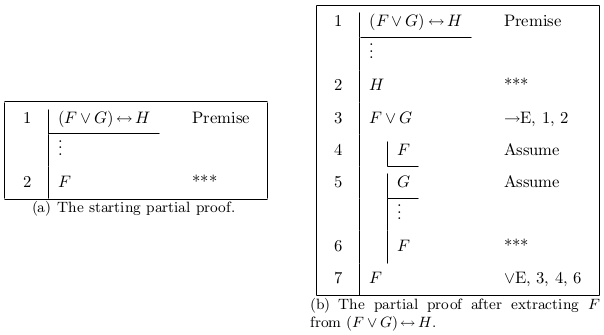
Figure 1.6: Using the extraction rule.

1.3 AProS: The Proof Generator

The AProS Proof Generator is an automated theorem prover that finds proofs in propositional and first-order logic [AProS website]. Making use of the intercalation calculus [Sieg, 1992, Sieg and Scheines, 1992, Sieg and Byrnes, 1998], its search style employs the previously-mentioned strategic proof search¹⁷. While the proof generator can be accessed independently through the Proof Display [AProS website], it can also be used by other programs as a library capable of producing strategically generated proofs. There are various ways in which the proof generator improves upon the basic strategic proof search; I note several here. For propositional logic these include: positive caching, negative caching, and careful selection of contradictory pairs. None of these improvements deviates from the aforementioned strategy. For first-order logic, the proof generator takes on a greater burden: it uses Skolem-Herbrand functions [Sieg and Byrnes, 1998, Enderton, 2001]. Also, it uses iterative deepening [Luger, 1997, pp. 106] to postpone traversing deep branches in the search space.

1.3.1 How to produce a tactical proof tree

We want to produce a tactical tree where each node 〈ϕ, t〉 has a formula (the goal of the rule application) and a tactic, and above each node are the open questions upon which that node depends. Given a natural deduction proof — obtainable from an intercalation calculus tree as mentioned in Section 1.2.2 — this is a straightforward recursive procedure starting from the goal and working upwards. For each non-extraction (non-↓) rule application, the goal is known and the above description of the tactics explains which tactic was used. The open questions are simply the premises of the intercalation calculus inference rule used in that step. For extraction moves (↓ rules) done in sequence, only one node is created, where ϕ is the goal of the bottommost extraction move and the open questions are the non-extraction dependencies of the rule applications in the sequence.

When this process is complete, the newly produced tree directly reflects the strategic moves used in the proof. Indeed, a preorder traversal¹⁸ of the tree gives a convenient step-by-step proof construction. When obtaining a proof from the proof generator, it is useful for the generator to retain some basic tactical information. In particular, extraction information is tedious to calculate after the fact. All of the other tactics are single rule applications, so one can determine their use simply by examining the current goal and the rule application associated with it. Regardless of how it is produced, a tactical tree is just what is needed to express AProS’s — or a student’s — moves in a strategic proof search.

1.4 The Carnegie Proof Lab

The design of the CPT was based on the belief that students learn more from exercises when their problem solving environment has three features. First, its interface must relieve the student of nonessential cognitive load. Second, it must allow students maximal flexibility in traversing the problem space. Third, it must provide locally appropriate strategic guidance. [Scheines and Sieg, 1994]

The Carnegie Proof Lab is a graphical proof construction environment. Written in Java, it is a multi-platform applet that is embedded into the Logic and Proofs course. The goal of the Carnegie Proof Lab is to make it easier for students to learn how to construct natural deduction proofs, and, once they can construct them, to prove harder problems with greater ease than on paper. See Figure 1.7 for a screenshot of the Carnegie Proof Lab.

Figure 1.7: The Carnegie Proof Lab.

There are several components to the Carnegie Proof Lab: the partial or complete proof, the rule palette, and the message display. A problem is complete when there are no open questions left in the proof. To use an inference rule, students select the goal and premises necessary for the inference rule and click the “apply” button. A major strength of the Carnegie Proof Lab is that it minimizes the load on working memory, so that the student may focus on the relevant information; see Anderson et al. [1995, pp. 180] for more on working memory constraints.

As students progress in the course, they are exposed to more inference rules. The full set of inference rules for propositional logic, seen in Figure 1.8, incrementally become available to the student during the semester; these are progressively displayed in the Carnegie Proof Lab.

Figure 1.8: The inference rule palette.

Additionally, students may optionally view the form of the rule — that is, the outlines shown in Appendix A — when determining what inference rule to apply. When students make errors using inference rules, they receive feedback on the nature of the error. See Figure 1.9 for an error where only one premise is selected for Conjunction Introduction.

Figure 1.9: A sample error message.

Specifically, an error is an attempted use of an inference rule in a manner not specified — for example, providing only one premise to Conjunction Introduction¹⁹. Using an inference rule that does not lead towards a completed proof does not produce an error message. According to Gilmore [1996, pp. 120], “the emphasis is not on how well the user achieves the current task goals, but on how well he or she learns about the nature of the task in some general abstract way”. It can be instructive, then, to allow students to use inference rules in valid but unproductive ways — indeed, a main point of strategic proof search is to provide students a means of identifying good rule applications, so it could be counterproductive to flag them as errors here.

In accordance with Gilmore [1996, pp. 131], this proof construction environment is designed to foster planning moves. Students select premises and choose inference rules without having to actually apply the rule until they are ready. The rule forms can be examined, so students may select the appropriate rule for the occasion. Indeed, the environment is designed to be transparent to the extent that students may modify the partial proof by properly using inference rules as they desire. This allows students to focus on how to connect the premises with the conclusion.

Chapter 2 Proof tutoring in propositional logic

The goal of the Proof Tutor is to provide high level advice for students on proofs with the intent that students will learn to incorporate techniques from hints into their own reasoning. In Logic and Proofs, strategic proof search, as described in the previous chapter, is used to produce this high level advice. While there are other heuristics and observations on methods of proofs that advanced students may determine from either other sources or direct observation of the proof search process, strategic proof search has several advantages in this setting, both following from its simplicity. First, although extraction has a somewhat complex precise formal explanation, it can be simply and informally expressed even to beginning students. The complexity of extraction is partly offset by the way in which both it and refutation make use of positively embedded subformulas. Second, the heuristic is quite effective at significantly reducing the search space. Other heuristics expressing ideas like “using Disjunction Introduction Left or Disjunction Introduction Right often leads to failure of the branch, so sometimes avoid these rules” or “using Existential Introduction before Existential Elimination often leads to variables not matching, so sometimes use Existential Elimination first” are useful in their own right, but they are less beneficial to students learning to construct proofs because they are more restricted in application and consequently less applicable overall, and clean expressions of these heuristics can be hard to produce.

Successful tutoring ought to be responsive to the skills of the student, and this holds for strategic proof tutoring just as it does elsewhere. To account for increasing skill as the student learns, then, there are three distinct proof tutoring levels or modes: tactical explanation, walking through a proof, and completing a partial proof. While these will be explored in greater detail in the following sections, I briefly note some key features here. A tactical explanation is a goal-specific piece of information explaining which tactics can currently be employed, walking through a proof provides an example of how to think strategically, and completing a partial proof provides students with on-demand hints. By sequentially making the tutoring modes available to the student, I hope to provide a reasonable level of broad support for learning how to strategically construct non-trivial proofs.

2.1 Tactical explanations in propositional logic

Successful problem solving involves the decomposition of the initial problem state into subgoals and bringing domain knowledge to bear on those goals. . . . [The] goal structure can be communicated through help messages [Corbett and Koedinger, 1997, pp. 867].

Some understanding of the key components of strategic proof search is necessary for using it, so the Explanation Tutor focuses on just this. In a problem with tactical explanations enabled, at any time the student may examine how the tactics could be applied. If the student has not selected a goal, the student is prompted to do so — Figure 2.1 shows a screenshot of this.

Figure 2.1: An explanation asking the student to select a goal.

Figure 2.2: The possible tactics for proving the goal.

When an open question is selected, the four tactics are listed, as shown in Figure 2.2. Each tactic name acts as a hyperlink, and when a hyperlink is selected, the corresponding tactic’s information is displayed in greater detail. This advice has two forms. Perhaps the tactic cannot be employed in the current circumstances, such as cases when there are no extractable disjunctions or existential formulas; this is shown in Figure 2.3. Alternately, the tactic may be immediately applicable. This is not to say the tactic will lead to a proof — indeed, in a proof of tertium non datur using inversion first will not lead to a proof of the proposition, but it is a legitimate use of the tactic. See Figure 2.4 for an example of this. An explanation of a tactic simply indicates whether a tactic is applicable given the current circumstances in the proof.

Figure 2.3: Explanation for an unusable tactic.

Figure 2.4: Explanation for inversion on P ∨ ¬P .

It may seem surprising that students receive explanations for tactics that do not lead to completed proofs, but this apparent discrepancy is resolved by reexamining the purpose of the tactical explanations. When students first learn the rules, they have a large search space of possible ac- tions. The tactics give them a way to restrict and simplify that space — from fourteen basic rules in propositional logic, only four tactics are produced. For a reasonable but arbitrary partial proof, it is desirable that students can look at the current open questions and determine which tactics can be employed, thus effectively conceptualizing the search space. According to Corbett and Koedinger [1997, pp. 859], “[the] student needs to learn basic declarative facts in a domain. . . . The student has to learn to associate these facts with problem solving goal structures”. Interestingly, because the Explanation Tutor offers a great deal of detail to students about the tactics, it can help students learn both the descriptions of the tactics — basic declarative facts — as well as the procedural skills involved with determining when the tactics can be used.

2.2 Walking through proofs in propositional logic

. . . when the teacher solves a problem before the class, he should dramatize his ideas a little and he should put to himself the same questions which he uses when helping the students. Thanks to such guidance, the student will eventually discover the right use of these questions and suggestions, and in doing so he will acquire something that is more important than the knowledge of any particular [fact]. [Polya, 1945]

In order for students to develop the ability to strategically produce proofs within the Carnegie Proof Lab, the Walkthrough Tutor is designed to provide step-by-step guidance from beginning to end on a proof. The Carnegie Proof Lab uses AProS to prove assertions, and hints are derived from the resultant proofs. Since one of the general goals is for students to learn strategic proof search, the Walkthrough Tutor provides hints on moves couched in strategic terms. Each tactic is expressible in one move in the Carnegie Proof Lab, and the tutor provides a hint for each move. These hints include premise and goal information, as well as a brief explanation of why the tactic ought to be used at that point. See Figure 2.5 for an example of an inversion step in a proof of tertium non datur.

Figure 2.5: Inversion advice on a subgoal of P ∨ ¬P .

It may happen that upon receiving a hint, the student still does not understand what is suggested. In this case, the student may click on the tactic for more details. The tactic name acts a hyperlink. Clicking on it opens a more detailed hint that, in addition to providing the strategic hint, also displays what rule should be applied to the specified premise and goal. See Figure 2.6 for the detailed hint for the same inversion step.

Figure 2.6: Detailed inversion advice on a subgoal of P ∨ ¬P .

This type of directed step-by-step performance feature is a well-recognized instructional intervention [Towne and Munro, 1992, Corbett and Koedinger, 1997]. When students are attempting to use strategic proof search on hard proofs, having examples to follow can be highly instructive. The value of examples in instruction has been reported elsewhere [Chi and Bassok, 1989, pp. 259], and in this setting it should also prove beneficial. When completing proofs for students in group or individual settings, the instructor generally explains things in terms of the tactics — “The goal is atomic, so there’s no way to use inversion here.” or “Look! Our goal is sitting inside of the second premise. Let’s try extraction.” — so having this type of explanation automated is reasonable.

As students start to learn strategic proof search, they may use the Walkthrough Tutor, but it may happen that they do not wish to follow the tutor’s advice. Perhaps they are at a point in the proof where the answer is evident, or perhaps they wish to try an inference rule that is not suggested. When students use an inference rule not suggested by the walkthrough — the walkthrough suggests only one inference rule — a warning message is displayed. The student is cautioned that they may well continue on their own to find a proof, but the walkthrough cannot help them, as seen in Figure 2.7.

Figure 2.7: The warning message for an offtrack move.

The student is then free to try completing the proof without assistance. Any time after this, though, the student may undo moves to get back to the point of deviation from the walkthrough. When the partial proof is back in the last recommended state — that is, when the off-track moves have all been undone — the walkthrough is re-enabled and the student may continue to follow it. Such antics on the student’s part may or may not lead to a completed proof, but the goal of the Walkthrough Tutor is not to force the student along the prescribed proof path, but to give the student enough structure to complete the proof strategically. Going off on tangents may have extra benefits to students — perhaps they are considering why particular moves were recommended, or perhaps they want to try to prove the problem in a different way. In any case, the student has fallback assistance, so the walkthrough continues to provide strategic and sufficient assistance for the student to complete the proof.

2.3 Completing proofs in propositional logic

When students are working through proofs in propositional logic, they sometimes get stuck and do not know what to do next. The aforementioned proof walkthroughs could be useful, but they require starting from the base partial proof, which does not take into account work already done by the student on the partial proof. The tactic explanations may also be of use. What would also be useful, though, is on-demand hints for particular moves in a proof. The Completion Tutor provides this type of tutoring. When students get stuck, they may ask for hints. Upon their doing so, the Carnegie Proof Lab examines the current partial proof. If the proof has not yet been started, it is treated just like a walkthrough — the first move is recommended. If the proof is non-normal, a hint is generated recommending the removal of the offending lines. Normal proofs are preferred not because non-normal proofs are incorrect, but because non-normal proofs have extra clutter that is both cumbersome to the student’s cognitive load as well as simply unnecessary. By removing non-normal proof steps, then, students benefit immediately, because there is less pointless information that may confuse them. They may also benefit on future problems, due to a hopefully improved ability to recognize these feckless non-normal steps for what they are.

2.3.1 Normalizing a proof

In order to provide strategic tutoring to a student with a partial proof, non-normal lines in the partial proof are undesirable and consequently removed. To make a non-normal partial proof normal, the simplest thing to do is to remove the non-normal rule applications from the partial proof — removing the lines produced by these as well as other lines dependent upon them from the partial proof produces a normal partial proof. See Appendix B for more on this algorithm and possible alternatives.

2.3.2 Cropping a proof

After removing non-normal lines in a partial proof, in order to provide a completion, the tutor must decide what other rule applications ought to be removed. If the student is working backwards, certain uses of Disjunction Introduction Left or Disjunction Introduction Right, say, can lead to unprovable goals. There are other ways to obtain states that require backtracking too, so it is important that these lines, as well as perhaps pointless or undesirable forwards rules, are removed. The key problem in completing a partial proof is determining what rule applications should be removed from P_u, the partial proof after normalization, before moving to have AProS complete the cropped partial proof P_c. The quality of a cropping algorithm is determined by how it fares at the following.

P_c must be completable.
P_c should complete to a reasonably short proof. This can be judged by comparing the length of that proof to the length of AProS’s proof of the original assertion.
The number of lines that are removed when going from P_u to P_c should be reasonably minimized.

There are many ways in which one can determine what rule applications to remove, so here we consider a simple algorithm that tries two things. It first checks to see if the current partial proof is completable by AProS, and, if so, the completed proof can be used. If not, it asks AProS for a proof of the starting assertion, and the rule applications that are in P_u but not in the completed proof are slated for removal. See Appendix B for more on this algorithm and possible alternatives.

2.3.3 Putting it together

Once a partial proof is normalized in some fashion and cropped as desired, then the correctness of the cropping algorithm ensures that AProS will be able to find a proof of the resultant partial proof. The tutor then takes the completed proof from AProS and produces a walkthrough (see Section 2.2) of it. The already-justified lines in the proof correspond to correct steps in the walkthrough, so the tutor skips over those. From this point, the tutor behaves just as it did for walkthroughs until the problem is complete. Of course, the student need not follow the walkthrough here until the proof is complete. If the student deviates from the walkthrough, the tutoring screen is set back to how it was before a hint was requested, so the student may return to tutoring later in the proof if desired.

The Completion Tutor thus provides on-demand tutoring at any stage in a problem. First of all, this enables students to complete the problem at hand. Second, and just as importantly, the tutoring is only present when students ask for it. This matches “Principle 8 [in designing computer-based tutoring systems]: Facilitate successive approximations to the target skill” [Anderson et al., 1995, pp. 181]. In keeping with the observations in [Anderson et al., 1995], it is expected that in this setting, students will ask for hints less of the time, in correspondence with increasing proof construction skills.

Chapter 3 Discussion

There are several areas of work that connect with dynamic proof tutoring in the Carnegie Proof Lab. This includes reflection on how best to use the tutor in Logic and Proofs, data analysis on the effect of its implementation, and a potential link to cognitive science research.

3.1 Incorporation into Logic and Proofs

The three tutoring modes emphasize connected but different aspects of strategic proof search; to use them effectively they must be deployed in appropriate ways. First, it is worth noting that the Completion Tutor and Walkthrough Tutor — because they rely on AProS to complete proofs — cannot be used on unprovable problems. The Explanation Tutor, on the other hand, doesn’t actually complete proofs, so it can be used for those problems. The Explanation Tutor only explains what tactics are currently applicable; thus, it can be enabled widely in the Carnegie Proof Lab without giving students excessive scaffolding. The Completion Tutor provides a reasonable amount of scaffolding — indeed, it will guide the student through an entire proof if the student so desires — and so should not be as extensively available. Still, it would be reasonable to have a handful of problems at the end of each chapter explicitly noted as Completion Tutor-enabled problems. Finally, to make use of the Walkthrough Tutor at all, students must follow its instructions explicitly. Because of this, it makes sense to have the Walkthrough Tutor available for a handful of in-chapter exercises — Learn by Doings — and perhaps a few exercises explicitly noted as such at the end of the chapter. These three modes can all be used starting with the first chapter on proof search²⁰. One can conceive of other ways of presenting problems to students — perhaps a problem selection engine that has skill thresholds for inference rules or tactics, where completing a problem without asking for a hint gives students a better score in the pertinent categories — in any case, the tutoring modes are to be deployed in a way where they initially provide a great deal of scaffolding and support decreases as students (presumably) become more skilled at strategic proof search.

3.2 Research into the Psychology of Proof

In Rips [1994], it is argued that certain aspects of human deductive reasoning can be effectively modeled through a kind of natural deduction proof search mechanism. Rips’s search engine, PSYCOP, is similar in character to AProS. As Sieg has noted [AProS website], both PSYCOP and the AProS search algorithm can be expressed as production rules — so it is conceivable to represent PSYCOP as a model in an ACT-R system²¹. To the degree that Rips is correct about PSYCOP as a model of deduction, there is significant motivation to study strategic proof search for that topic alone.

3.3 Extensions

While some of the tutoring-related features described here have been in use for the past year, the tutors themselves will be used in a semester-length version of the course for the first time Fall 2007. By analyzing the logging data produced by students using the Carnegie Proof Lab — with a computer-based problem-solving environment, it is feasible to gather detailed, extensive data — it is possible to ascertain what tutoring modes are used by and useful to the students. For instance, suppose the Completion Tutor is available for five assigned problems at the end of some chapter. Suppose students are having difficulty on problems of comparable difficulty, and use the Completion Tutor when needed. If the Completion Tutor is effective, then one would predict that the need for the Completion Tutor will decrease and that fewer mistakes will be made. This should happen anyway, at least for students who are learning by problem solving, but the rate of decrease will rise in proportion to the Completion Tutor’s effectiveness²². For students who are not making progress through repeated exposure to proofs without tutoring, the Completion Tutor can be even more valuable.

The propositional tutor for the Carnegie Proof Lab has been implemented, and some details of how it could be extended to first-order logic have been explored — see Appendix B for more on this. The Explanation Tutor already works for first-order logic, and the Walkthrough Tutor can readily be made to find proofs in first-order logic. The Completion Tutor, on the other hand, may not be so easily extendable to first-order logic, because AProS uses Skolem-Herbrand variables, but students in the Carnegie Proof Lab do not. Other difficulties may also arise. For instance, when describing Universal Elimination, it is necessary to sensibly display information on instantiating variables. For longer extraction branches, this could require substantial modification to the current framework. The same concern exists for Universal Introduction and Existential Introduction. Also, because students are exposed to first-order logic several weeks after working on strategic proof search in propositional logic, some aspects of strategic proof search do not need to be emphasized as much as others.

Some current work on the AProS project involves work on selected parts of elementary set theory and computability theory; see Sieg [2007]. Parts of the Logic and Proofs course will be combined with twelve new chapters — six on elementary set theory and six on computability theory. In combination with this, AProS has been and will continue to be extended to deal with proofs of certain theorems in these areas. AProS can be used to produce hints in propositional and first-order logic, and the Carnegie Proof Lab can use AProS to generate hints for proof construction in these logics; similarly, as AProS and the Carnegie Proof Lab are modified to incorporate the appropriate parts of elementary set theory and computability, it may be possible to use AProS as a hint generator in this extended setting much as it works in the current one.

Appendix A Inference Rules

The inference rules for propositional logic are as follows.

Conjunction Elimination Left
Conjunction Elimination Right
Conjunction Introduction
Disjunction Elimination: ρ may be ⊥. It may also be noted that Disjunction Elimination can be used from premises and assumptions that are disjunctions as well as strictly positively embedded disjunctions. In the case that the desired disjunction is not immediately available, an extraction branch is produced leading to the disjunction, and Disjunction Elimination is applied on that disjunction and the specified goal.
Disjunction Introduction Left
Disjunction Introduction Right
Implication Elimination
Implication Introduction
Biconditional Elimination Left: Because the biconditional can be written in terms of a conjunction of conditionals, it is often omitted from discussion. For convenience, though, it may be used in Logic and Proofs.
Biconditional Elimination Right
Biconditional Introduction
Negation Elimination
Negation Introduction
Falsum Introduction
Ex falso quodlibet: Ex falso quodlibet is not one of the basic rules in the Carnegie Proof Lab, but it would be if one were to use the Carnegie Proof Lab for intuitionistic logic.

The following are the first-order logic inference rules.

Universal Elimination: t must replace all free instances of x in ϕ. Let the syntax ϕ[t/x] denote the formula ϕ where all free instances of x have been replaced with t. This is called substituting t for x.
Universal Introduction: x must replace all free instances of z in ϕ(z), and z must not occur free in any assumption upon which line b depends.
Existential Elimination: z must not be free in (∃x)ϕ or ψ and z must not occur free in any assumption upon which line d depends. ρ may be ⊥.
Existential Introduction

Appendix B Algorithms

Although proof tutoring currently works just for propositional logic, it is possible to extend it to first-order logic. Thus, the algorithms described here are defined for both propositional logic and first-order logic where appropriate.

Partial proof normalization

In propositional logic, given a partial proof with non-normal steps, one can examine it and easily determine the pairs of inference rule applications that violate the adjacency condition or are not p-normal. Given this list of pairs, there are two reasonable methods for normalizing the proof.

For each pair of inference rule applications, one can normalize the partial proof much as one would if it were a completed proof. If the pair involves Conjunction Introduction on ϕ₁ and ϕ₂ and Conjunction Elimination to ρ, then either ϕ₁ or ϕ₂ has a formula equal to ρ and should be used in place of ρ. If the pair involves Disjunction Introduction on some premise ϕ and then Disjunction Elimination to ρ, then the two subproofs that resulted from Disjunction Elimination should be removed, and the work in the subproof with the assumption whose formula equals ϕ should be moved to below ϕ and above ρ. For Negation Elimination on ϕ just above Falsum Introduction, the two rule applications are removed, and work done inside the subproof (from ¬ϕ to ⊥) is adjusted to connect with the goal of the Falsum Introduction rule application. Negation Introduction is treated similarly. Fortunately, because there are no other ways of producing non-normal proofs in the Carnegie Proof Lab with the basic inference rules²³, the above cases are the only ways students could produce non-normal partial proofs. For first-order logic, it is also necessary to consider pairs of existential and universal introduction and elimination. For Universal Introduction on ϕ(x) to Universal Elimination with goal ϕ(y), one can remove the two rule applications and use ϕ(x) in place of ϕ(y). For Existential Introduction on ϕ(x) to Existential Elimination with premise ϕ(y) and goal ρ, any work done below ϕ(y) can be moved below ϕ(x) and y suitably replaced with x.
To make a partial proof normal, one can simply remove the pairs of inference rule applications that make it non-normal. In the case of Conjunction Introduction and Conjunction Elimination pairs, any dependencies below the rule applications must also be removed. For Disjunction Introduction and Disjunction Elimination pairs, it is necessary to remove the two rule applications and the subproofs that resulted from Disjunction Elimination. For Falsum Introduction and either Negation Introduction or Negation Elimination, the two rule applications and the subproof created by Negation Introduction or Negation Elimination are removed. For Existential Introduction and Existential Elimination pairs, the two rule applications and the subproof are removed. This process may remove potentially large segments of the partial proof, if a significant amount of work is dependent on a non-normal pair of rule applications.

Either algorithm is sufficient for the goals here, since the only requirement is to reasonably produce a normal partial proof.

Partial proof cropping

To crop a normal partial proof P_u and produce a new partial proof P_c satisfying the invariants in Section 2.3.2, there are many possible solutions; we consider several here.

Obtain a proof of the base assertion from AProS. Retain the student’s work only to the extent that it matches AProS’s proof.
Attempt to complete the partial proof P_u using AProS. If such a proof is obtainable, do not remove anything. If it is not obtainable, then use algorithm 1.
It is possible to modify algorithm 2 in a small but useful way. Attempt to complete the partial proof P_u using AProS. If a proof is obtained, then do not remove anything. If not, obtain a proof of the base assertion from AProS. Determine the spot where the student’s proof first diverges from this proof, and note the first rule application made by the student and not by AProS. Then ask AProS to complete the partial proof that includes the overlap between the proof and the partial proof with the addition of the rule application just mentioned. If AProS succeeds, retain all work consistent with this new proof. If not, use algorithm 1.
One can also brute-force the entire operation. For the current partial proof, use AProS to attempt to complete it. If AProS succeeds, then do not remove anything. If not, then consider removing the rule application that produced the current goal²⁴. Now try to complete this partial proof. Keep removing goals until a proof is found. Once a proof is found, retain all work consistent with it. In the worst case, this algorithm acts like algorithm 2.

All of the algorithms just mentioned fulfill the requirement, though they obviously have different strengths. It is clear that algorithm 1 is sometimes too simple and algorithm 4 may be too computationally intensive, depending on the implementation, so perhaps one of the middle algorithms — or a modification thereof — is desirable in practice. For first-order logic, if P_u is not completable, it is possible that AProS will search indefinitely for a proof. One could modify the algorithms for completing partial proofs, though, by placing a cap on the depth of the tree — the number of inference rules applied in the completed proof — at, say, one hundred inference rule applications. Proofs in the Carnegie Proof Lab are typically for problems of shorter length than this, so such an upper bound is reasonable.

It may often be possible to classify certain kinds of unwanted rule applications. For instance, algorithm 1 will always crop forwards introduction moves, so one could provide more detailed feedback specifically addressing the in-principle undesirability of such rule applications. The other large class of rule applications leading to cropping are backwards rules that lead to partial proof graphs for which backtracking is necessary. It is also possible to more reasonably articulate backtracking steps in cropping, though in general it is difficult to clearly explain why a particular rule application led to a failed branch.

Footnotes

1. See Chi et al. [1994] for more on the value of self-explanation.
2. Small exercises may be useful for helping students learn how to use a method and identify broad misunderstandings about the method.
3. Let us somewhat arbitrarily say that a complex proof involves perhaps five or more nested subproofs and many different inference rules, while a long proof is perhaps twenty to thirty-five lines long.
4. In some standard presentations, Prawitz [1965] and van Dalen [2004], e.g., ⊥ is an atomic formula, and ¬ϕ is shorthand for ϕ → ⊥. This is distinct from Logic and Proofs, where ⊥ is not used in building complex formulas and, consequently, ¬ϕ cannot be rewritten as ϕ → ⊥.
5. More precisely, Logic and Proofs places subproofs in whole boxes, a notation used by Jàskowski in 1934, later dropped due to typesetting hassles and replaced by vertical bars on the left side of the proof [Pelletier, 1999]. Fitch’s notation is standard today, and it is similar enough to Jàskowski’s that a reader familiar with the first should have no trouble reading proofs in the second.
6. See Harper [2007, pp. 4] for a formal definition of inference rules.
7. Only Negation Elimination and Falsum Introduction are formulated differently; see Appendix A.
8. Intuitionistic logic is briefly mentioned in Logic and Proofs, but the topic is not extensively pursued there, so neither will it be here.
9. This change is necessary because of minor differences in formulation of the negation rules. In Sieg and Byrnes [1998], the falsum, ⊥, is not used. In Logic and Proofs its use is highly restricted.
10. Also, one could disallow the minor premise to be the conclusion of Negation Elimination. Say the goal is ⊥ and a contradictory pair is chosen, ϕ and ¬ϕ. Trying to prove ϕ by Negation Elimination means assuming ¬ϕ and trying to prove a contradiction. However, ¬ϕ needs to be proven anyway, so assuming it in the subproof is not helpful. That is, if ¬ϕ can be proven, and by assuming ¬ϕ one can infer ⊥, then one can prove ⊥ without that use of Negation Elimination. This is stronger than normality as defined in Sieg and Byrnes [1998] or Prawitz [1965], though.
11. Here I only cover the intercalation calculus for classical propositional logic, though the modifications necessary for intuitionistic or first-order logic match earlier discussion on these logics; see the aforementioned references for descriptions of the intercalation calculus for intuitionistic and first-order logic.
12. With the inference rules specified here, there are only a few ways to obtain repeated questions. If one applies an inference rule when the rule has already been used on the same premises and goal below the current node in the search tree, this is a repeated question and should not be pursued.
13. Using ¬C will not lead to a proof on the left or center node, but it is permissible.
14. See Sieg and Byrnes [1998] for a precise description of search space tree evaluation.
15. Because of the formulation of the inference rules and the prohibition of duplicate questions, the search space and search tree are finite.
16. See Appendix A for details on strictly positively embedded premises and assumptions.
17. As of June 2007, in a few corner cases AProS is not as restrictive as the specification — AProS does not restrict Negation Introduction or Negation Elimination according to the adjacency condition.
18. A preorder traversal of a tree is defined recursively. Starting at the root, visit the current node, then visit each of the children from left to right. Polish notation is a preorder traversal of the evaluation tree. See Cormen et al. [2004, pp. 254] or various data structures textbooks for examples.
19. This is contrasted with non-strategic rule applications, which are permitted. For instance, even though using
Conjunction Introduction does not follow the aforementioned strategy, it is nonetheless permitted.
20. In the first chapter on proof search, the negation rules aren’t available yet, so the tutoring modes should not indicate it. In fact, only the Explanation Tutor needs any modification to achieve this.
21. See Anderson [1993] for more on the ACT-R theory.
22. In Scheines and Sieg [1994], the effect of strategic tutoring in the Carnegie Proof Tutor, the Carnegie Proof Lab’s predecessor, is noted. It was observed there that on hard problems, strategic tutoring can be greatly beneficial, and we expect to observe similar results with tutoring in the Carnegie Proof Lab.
23. There is no way for students to arbitrarily make assumptions; thus, Implication Introduction and Biconditional Introduction cannot be used in a forwards direction.
24. There may be multiple open questions; an implementation of this or the previous algorithm would have to choose a good approach for dealing with multiple goals.

Bibliography

John R. Anderson. Rules of the Mind. Erlbaum, Hillsdale, NJ, 1993.
John R. Anderson, Albert T. Corbett, Kenneth R. Koedinger, and Ray Pelletier. Cognitive tutors: Lessons learned. The Journal of the Learning Sciences, 4(2):167–207, 1995.
AProS website. AProS: Automated Proof Search. Carnegie Mellon University, Philosophy Department, project website since 2004, 2006. URL http://www.phil.cmu.edu/projects/apros/.
Michelene T. H. Chi and Miriam Bassok. Learning from examples via self-explanations. In Lauren B. Resnick, editor, Knowing, learning, and instruction: Essays in honor of Robert Glaser, pages 251–282. Erlbaum, Hillsdale, NJ, 1989.
Michelene T. H. Chi, Nicholas De Leeuw, Mei-Hung Chiu, and Christian Lavancher. Eliciting self-explanations improves understanding. Cognitive Science, 18(3):439–477, 1994.
Albert T. Corbett and Kenneth R. Koedinger. Intelligent tutoring systems. In Martin Helander, T. K. Landauer, and P. Prabhu, editors, Handbook of Human-Computer Interaction, pages 849–874. Elsevier Science B.V., St. Louis, 1997.
Thomas H. Cormen, Charles E. Leiserson, Ronald R. Rivest, and Clifford Stein. Introduction to Algorithms. MIT Press, Cambridge, MA, second edition, 2004. ISBN 0-262-03293-7.
Herbert B. Enderton. A Mathematical Introduction to Logic. Harcourt Academic Press, Burlington, MA, second edition, 2001. ISBN 0-12-238452-0.
Flash website. Adobe flash player. Macromedia website, 2007. URL http://www.macromedia.com/software/flash/about/.
Gerhard Gentzen. Investigations into logical deduction. In M. E. Szabo, editor, The Collected Papers of Gerhard Gentzen, pages 68–128. North-Holland, 1969. Written in 1934.
David J. Gilmore. The relevance of HCI guidelines for educational interfaces. Machine-Mediated Learning, 5(2):119–133, 1996.
Robert Harper. Practical Foundations for Programming Languages. Carnegie Mellon University, Pittsburgh, PA, draft edition, 2007. URL http://www.cs.cmu.edu/~rwh/plbook/. Updated 10 April 2007.
George F. Luger. Artificial Intelligence: Structures and Strategies for Complex Problem Solving. Pearson Education Limited, Essex, fourth edition, 1997. ISBN 0201-64866-0.
Open Learning Initiative website. Open Learning Initiative: Logic & Proofs. Carnegie Mellon University, course website since 2003, 2006. URL http://www.cmu.edu/oli/courses/enter_logic.html.
Francis J. Pelletier. A brief history of Natural Deduction. History and Philosophy of Logic, 20: 1–31, 1999.
G. Polya. How To Solve It. Princeton University Press, Princeton, NJ, second edition, 1945.
Dag Prawitz. Natural Deduction: A Proof-Theoretic Study. Almqvist & Wiksell, Stockholm, 1965.
Lance J. Rips. Psychology of Proof. MIT Press, Cambridge, MA, 1994. ISBN 978-0262181532.
Richard Scheines and Wilfried Sieg. Computer environments for proof construction. Interactive Learning Environments, 4(2):159–169, 1994.
Wilfried Sieg. Mechanisms and Search (Aspects of Proof Theory). AILA Preprint, Milan, 1992.
Wilfried Sieg. The structure of normal proofs and automated search. Manuscript, August 2005.
Wilfried Sieg. The AProS project: Strategic thinking and computational logic. To appear in Logic Journal of the IGPL, draft, 2007.
Wilfried Sieg and John Byrnes. Normal natural deduction proofs (in classical logic). Studia Logica, 60(1):67–106, 1998.
Wilfried Sieg and Clinton Field. Automated search for Gödel’s proofs. Annals of Pure and Applied Logic, 133(1):319–338, 2005.
Wilfried Sieg and Richard Scheines. Searching for proofs (in sentential logic). In Leslie Burkholder, editor, Philosophy and the Computer. Westview Press, Boulder, 1992.
Douglas M. Towne and Allen Munro. Supporting diverse instructional strategies in a simulation-oriented training environment. In J. Regian and V. Shute, editors, Cognitive Approaches to Automated Instruction. Lawrence Erlbaum Associates, Hillsdale, NJ, 1992.
Dirk van Dalen. Logic and Structure. Springer, Berlin, fourth edition, 2004. ISBN 3-540-20879-8.